Revisão de Matemática - 1º parte

CAP. 04 P. 104 À 110

Casos de semelhança de triângulos

.Para que dois polígonos sejam semelhantes, são necessárias duas condições:

                                    

                                        01-Todos os ângulos devem ser ordenadamente congruentes.

02-Os lados correspondentes devem ser proporcionais

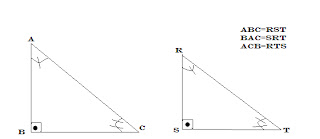
1º caso: AA (ângulo - ângulo)

. Dois triângulos que possuem dois ângulos ordenadamente congruentes são semelhantes.

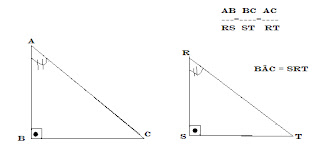
2º caso: LAL (lado - ângulo - lado)]

. Se dois triângulos possuem dois pares de lados homólogos (iguais) proporcionais e se os ângulos formados por esses pares de lados são congruentes, então os triângulos são semelhantes.

3ºcaso: LLL (lado - lado - lado)

. dois triângulos são semelhantes se possuem os lados homólogos proporcionais

CAP 10 P. 288 À 300

01-Elementos da circunferência

Circunferência é o conjunto de todos os pontos de um plano que são equidistantes de um ponto fixo, que é o centro da circunferência.

Seus elementos:. O ponto O é o centro da circunferência;

. O segmento OC é o raio;

. O segmento CA é o diâmetro;

. O segmento DE é uma corda;

. Os pontos D e E dividem a circunferência em dois raios DE e ECD.

02-Posições relativas entre reta e circunferência coplanares

.Retas e circunferência secantes:

. A reta é secante à circunferência, quando a distância do ponto central até a reta é menor que a medida do raio.

OBS: Uma reta e uma circunferência secantes possuem apenas dois pontos em comum:

. Sendo um corda determinada por uma circunferência e uma reta secante.

. O raio perpendicular à secante passa pelo ponto médio da corda.

.Retas e circunferências tangentes. A reta é tangente a circunferência, quando a distância do ponto central até a reta é igual a medida do raio.

OBS: Uma reta e uma circunferência tangentes possuem apenas um ponto em comum:

. O raio da circunferência é perpendicular a reta tangente no ponto de tangência.

By: Kathlyn